Для определения натуральной величины угла между скрещивающимися прямыми, можно выполнить замену плоскостей так, чтобы обе прямые были параллельны плоскости проекций, или ввести обе прямые в одну плоскость и решить задачу для угла между пересекающимися прямыми.
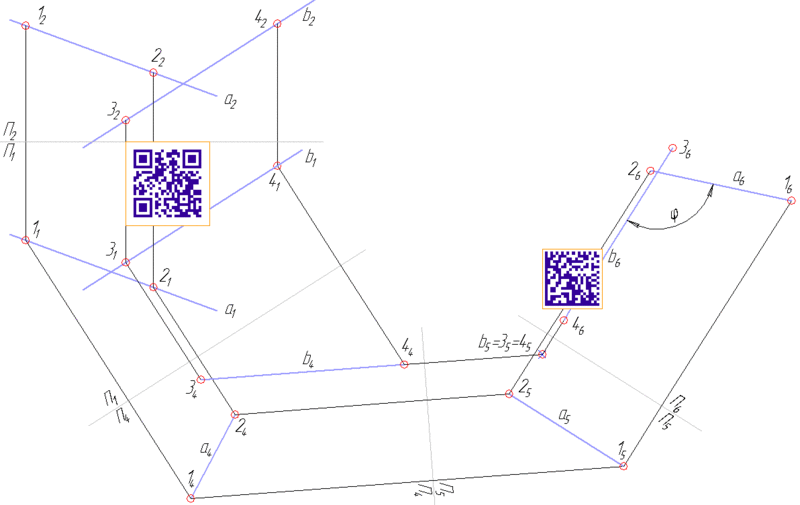
Тремя заменами плоскостей проекций преобразуется чертёж так, что обе заданные прямые становятся параллельны плоскости проекций.
Первая замена - плоскость проекции проводится параллельно прямой b. Вторая замена - перпендикулярно той же прямой b, которая занимает проецирующее положение и её проекция выражается точкой. Третья замена - параллельно прямой a. Так как после второй замены, прямая b занимает проецирующее положение, то любая замена приведёт к тому, что эта прямая b будет параллельна плоскости проекций. Таким образом, после третьей замены, найдено такое положение, что обе прямые параллельны плоскости проекций.
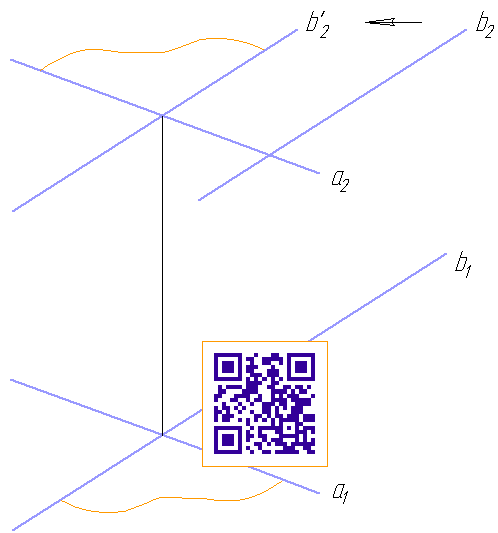
Скрещивающиеся прямые вводятся в одну плоскость путём проведения параллельной к одной из заданных прямой линии так, что бы точки пересечения проекций имели проекционную связь. Угол между скрещивающимися прямыми может быть найден методами подходящими для плоской фигуры и определения натуральной величины угла между прямыми.