Натуральную величину отрезка АВ можно найти методами: замены плоскостей проекций, вращения вокруг проецирующей оси и методом прямоугольного треугольника. Замена плоскостей и вращение позволяют преобразовать чертёж так, что проекция равна натуральной величине отрезка АВ. Метод прямоугольного треугольника позволяет найти отрезок равный величине АВ повторяя геометрические построения метода замены плоскостей проекций.
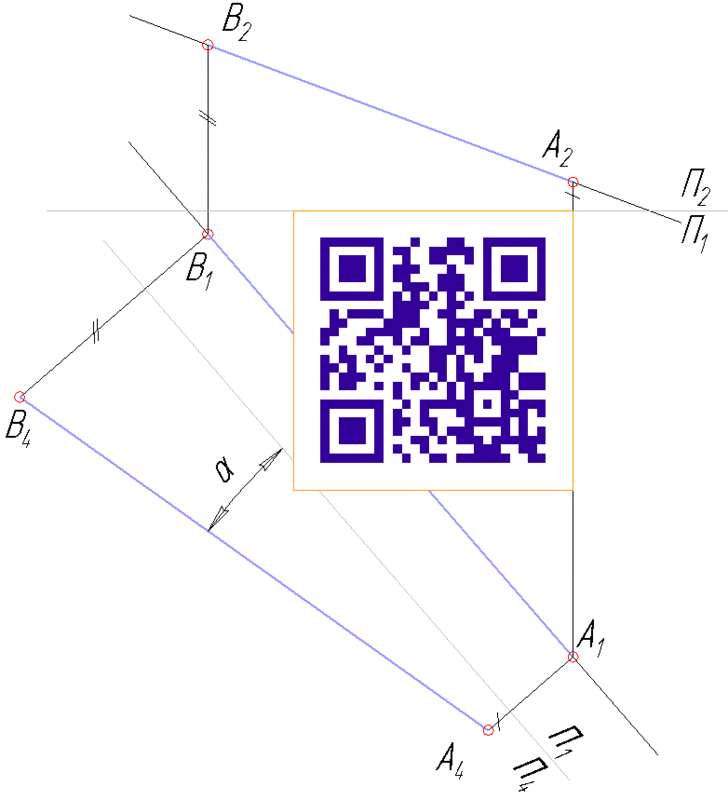
Замена фронтальной плоскости проекций П1/П2→П5/П2, П5║АВ позволяет найти натуральную величину отрезка равную A5B5.

Один из концов отрезка можно повернуть вокруг оси проходящей через другой конец отрезка и перпендикулярной плоскости проекций. Вращение выполняется до нахождения положения параллельного плоскости проекций. Траектория вращения представляется окружностью на одной проекции и прямой линией параллельной оси пересечения плоскостей проекций.
На примере эпюра отрезка, вращение отрезка выполнено до нахождения фронтали. Натуральная величина АВ равна фронтальной проекции отрезка.

Горизонтальная проекция отрезка выбрана в качестве катета основания прямоугольного треугольника. Вторым катетом взят отрезок равный высоте АВ. Гипотенуза полученного прямоугольного треугольника находит натуральную величину отрезка.